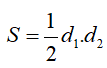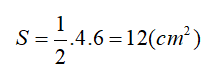Lớp 1
Đề thi lớp 1
Lớp 2
Lớp 2 – Kết nối tri thức
Lớp 2 – Chân trời sáng tạo
Lớp 2 – Cánh diều
Tài liệu tham khảo
Lớp 3
Lớp 3 – Kết nối tri thức
Lớp 3 – Chân trời sáng tạo
Lớp 3 – Cánh diều
Tài liệu tham khảo
Lớp 4
Sách giáo khoa
Sách/Vở bài tập
Đề thi
Lớp 5
Sách giáo khoa
Sách/Vở bài tập
Đề thi
Lớp 6
Lớp 6 – Kết nối tri thức
Lớp 6 – Chân trời sáng tạo
Lớp 6 – Cánh diều
Sách/Vở bài tập
Đề thi
Chuyên đề & Trắc nghiệm
Lớp 7
Lớp 7 – Kết nối tri thức
Lớp 7 – Chân trời sáng tạo
Lớp 7 – Cánh diều
Sách/Vở bài tập
Đề thi
Chuyên đề & Trắc nghiệm
Lớp 8
Sách giáo khoa
Sách/Vở bài tập
Đề thi
Chuyên đề & Trắc nghiệm
Lớp 9
Sách giáo khoa
Sách/Vở bài tập
Đề thi
Chuyên đề & Trắc nghiệm
Lớp 10
Lớp 10 – Kết nối tri thức
Lớp 10 – Chân trời sáng tạo
Lớp 10 – Cánh diều
Sách/Vở bài tập
Đề thi
Chuyên đề & Trắc nghiệm
Lớp 11
Sách giáo khoa
Sách/Vở bài tập
Đề thi
Chuyên đề & Trắc nghiệm
Lớp 12
Sách giáo khoa
Sách/Vở bài tập
Đề thi
Chuyên đề & Trắc nghiệm
IT
Ngữ pháp Tiếng Anh
Lập trình Java
Phát triển web
Lập trình C, C++, Python
Cơ sở dữ liệu

Công thức, Định nghĩa Toán, Lí, HóaĐường thẳngHình tam giácCác trường hợp tam giác bằng nhauHình thangHình bình hànhHình thoiHình chữ nhật
Hình thoi là gì ? Định nghĩa, Tính chất về Hình thoi chi tiết
Trang trước
Trang sau
1.Định nghĩa
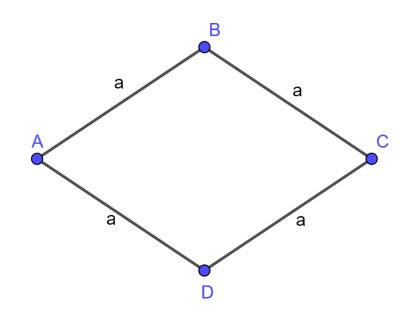
Hình thoi là tứ giác có bốn cạnh bằng nhau
ABCD là hình thoi AB = BC = CD = DA .
Đang xem: Hình nào là hình thoi
2.Tính chất
•Hai đường chéo vuông góc với nhau.
ABCD là hình thoi:
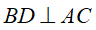
•Hai đường chéo là các đường phân giác của các góc của hình thoi.
ABCD là hình thoi: AC là đường phân giác của góc
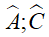
và BD là đường phân giác của góc
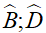
Hình thoi có tất cả các tính chất của hình bình hành.
3.Dấu hiệu nhận biết
•Tứ giác có bốn cạnh bằng nhau là hình thoi.
•Tứ giác có hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường là hình thoi.
•Hình bình hành có hai cạnh kề bằng nhau là hình thoi.
•Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.
•Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.
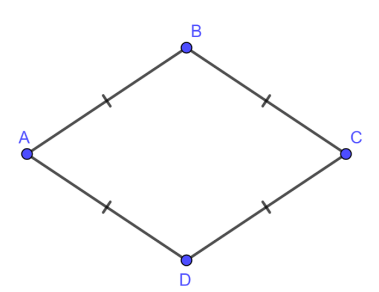
Ví dụ 1: Trong các hình sau, hình nào là hình thoi? Vì sao?
Hướng dẫn:
a)Tứ giác ABCD có AB = BC = CD = DA nên ABCD là hình thoi
b)Tứ giác ABCD có AB = CD, AD = BC nên ABCD là hình bình hành.
Xem thêm: 100+ Cách Đặt Tên Con Gái, Tên Con Gái Đẹp Hay Và Ý Nghĩa Theo Phong Thủy
Hình bình hành ABCD có đường chéo AC là đường phân giác góc
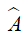
nên ABCD là hình thoi.
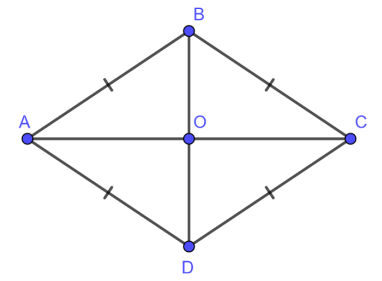
c)Tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau tại trung điểm của mỗi đường nên ABCD là hình thoi
d)Ta có: B, C, D đều thuộc đường tròn tâm A nên AB = AC = AD (1)
A, C, D đều thuộc đường tròn tâm B nên AB = BC = BD (2)
Từ (1) và (2) suy ra, AC = AD = BC = BD
Do đó, ABCD là hình thoi.
e)Tứ giác ABCD có các cạnh đối diện không bằng nhau, do đó ABCD không là hình thoi.
4.Diện tích hình thoi
•Dựa vào cạnh đáy và chiều cao tương ứng
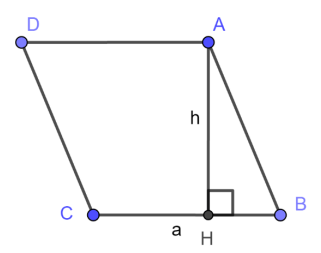
Vì hình thoi cũng là hình bình hành nên ta có thể tính diện tích hình thoi tương tự như hình bình hành. Diện tích hình thoi bằng tích của chiều cao nhân với cạnh đáy tương ứng.
S = a.h
h: độ dài chiều cao của hình thoi
a: độ dài cạnh đáy tương ứng
•Dựa vào hai đường chéo
Diện tích hình thoi còn có thể tính theo cách khác đó là dựa vào độ dài hai đường chéo. Diện tích hình thoi bằng một nửa tích hai đường chéo của nó.
d1, d2 : là độ dài hai đường chéo của hình thoi.
Ví dụ 2: Cho hình thoi ABCD có AB = BC = CD = DA = 4cm, chiều cao hình thoi bằng 3cm. Tính diện tích hình thoi.
Hướng dẫn:
Áp dụng công thức tính diện tích hình thoi khi biết cạnh đáy và chiều cao ta có a = 4cm, h = 3cm. Diện tích hình thoi ABCD là: 4.3 = 12 (cm2)
Ví dụ 3: Tính diện tích hình thoi ABCD biết độ dài hai đường chéo của hình thoi lần lượt là 4cm và 6cm.
Xem thêm: Kỹ Thuật Chụp Ảnh Cơ Bản – Kỹ Thuật Chụp Ảnh Ngược Sáng Đẹp
Hướng dẫn:
Áp dụng công thức tính diện tích hình thoi khi biết độ dài hai đường chéo, ta có diện tích hình thoi ABCD là:
5.Chu vi hình thoi
Chu vi của hình thoi bằng tổng độ dài bốn cạnh của hình thoi (hay chu vi hình thoi bằng độ dài một cạnh nhân với 4)
Ví dụ 4: Cho hình thoi ABCD có AB = BC = CD = DA = 5cm. Tính diện tích hình thoi.
Hướng dẫn:
Áp dụng công thức ta có chu vi hình thoi ABCD là:
P = 4.5 = 20(cm)
Giới thiệu kênh Youtube myalbum.vn
CHỈ CÒN 250K 1 KHÓA HỌC BẤT KÌ, myalbum.vn HỖ TRỢ DỊCH COVID
Phụ huynh đăng ký mua khóa học lớp 6 cho con, được tặng miễn phí khóa ôn thi học kì. Cha mẹ hãy đăng ký học thử cho con và được tư vấn miễn phí. Đăng ký ngay!